New particle at last! Physicists detect the first “glueball”

When it comes to the Standard Model of particle physics, most people incorrectly assume that it’s known, it’s correct, and that there are no more open questions about its validity. While the Standard Model has certainly withstood every challenge that’s been thrown at it by way of direct detection experiments, there are still a whole slew of questions that have yet to be answered. Although the matter that makes us up is composed of atoms, which are made of protons, neutrons, and electrons, and where the protons and neutrons are made up of three quarks apiece — all held together by gluons through the strong interaction — that’s not the only possible way to have bound states of matter.

In theory, at least according to quantum chromodynamics (our theory of the strong nuclear force), there should be multiple ways to make a bound state of quarks, antiquarks, and/or gluons alone.

• You can have baryons (with 3 quarks each) or anti-baryons (with 3 antiquarks each).
• You can have mesons (with a quark-antiquark pair).
• You can have exotic states like tetraquarks (2 quarks and 2 antiquarks), pentaquarks (4 quarks and 1 antiquark or 1 quark and 4 antiquarks), or hexaquarks (6 quarks, 3 quarks and 3 antiquarks, or 6 antiquarks), etc.
• Or, you can also have states made of gluons alone — with no valence quarks or antiquarks — known a glueballs.

In a radical new paper just published in the journal Physical Review Letters, the BES III collaboration just announced that an exotic particle, previously identified as the X(2370), may indeed be the lightest glueball predicted by the Standard Model. Here’s the science of the claim, as well as what it all means.

Bubble chamber tracks from Fermilab, revealing the charge, mass, energy, and momentum of the particles and antiparticles created. Although we can reconstruct what happened at the collision point for any one event, we need large numbers of statistics to build up sufficient evidence to claim the existence of any new particle species.

If you want to find a particle in the world of high-energy physics, it isn’t enough to simply create that particle in the lab and build a detector around it, viewing the decay products and determining what occurred back at the point of that particle’s creation. The problem with that approach is that, in a quantum Universe, there’s rarely a single definitive outcome that you can predict based on a set of given initial conditions. Instead, you can only predict the probabilities of a wide variety of outcomes that are expected to occur, and then you require many repeated observations to determine whether your theoretical predictions align with or conflict with what you observe.

This becomes especially important when you’re looking for something that should exist or occur within the Standard Model, but only under infrequent, possibly special conditions or circumstances. Every unstable particle — both fundamental and composite — has a set of decays that it’s allowed to experience, and a frequency for each decay pathway that’s also predicted: known as its branching ratios. While we normally think of particle creation as occurring only if you have enough energy to make it from energy, via Einstein’s famous E = mc², the reality is that many composite particles can only be detected from the signatures left when other known particles are created in great numbers, and then decay away.

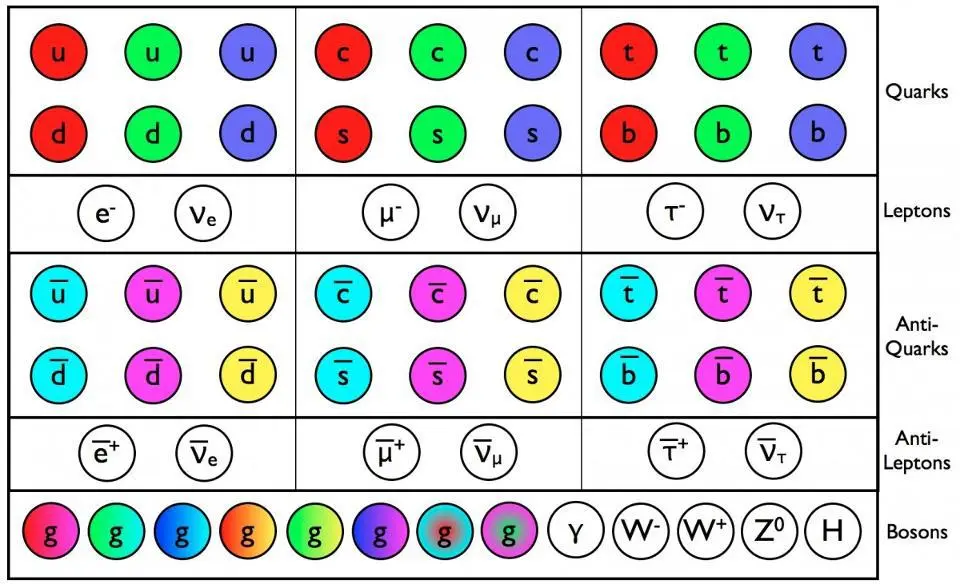
The particles and antiparticles of the Standard Model have now all been directly detected, with the last holdout, the Higgs boson, falling at the LHC in 2012. Today, only the gluons and photons are massless; everything else has a non-zero rest mass. Only the quarks and gluons couple to the strong force, and experience QCD interactions.

During the 20th century, various pieces of the Standard Model came together. We discovered that atoms were composed of nuclei and electrons, and then that the atomic nuclei themselves were made of still smaller particles: protons and neutrons, which were further divisible into quarks and gluons. It was soon determined that there weren’t just two types of quarks — the up and down flavors — but heavier, exotic, short-lived types as well.

• The first particle to contain a strange quark, the kaon, was discovered in 1947, but the explanation for it (including the existence of the strange quark) was only found in 1964.
• The first discovery of the charm quark came in 1974, when a particle known as the J/ψ was discovered by two independent teams: Samuel Ting’s team at Brookhaven (who named it “J” after himself, as the Chinese character for Ting is 丁) and Burton Richter’s team at SLAC (who named it “ψ” consistent with other conventions in particle physics).
• The bottom quark was discovered soon thereafter in 1977, and the sixth and final quark predicted by the Standard Model, the top quark, was revealed in 1995.

All particles that are composed of any of these heavier, exotic quarks (or antiquarks) are fundamentally unstable, and must not only decay, but decay through the weak interactions in order to change the species of the constituent quarks inside. All particles containing a strange, charm, bottom, or top quark cannot remain stable for long; in a tiny fraction of a second, they decay and change species, transitioning back into lower-energy, lighter, more stable particles in the process.

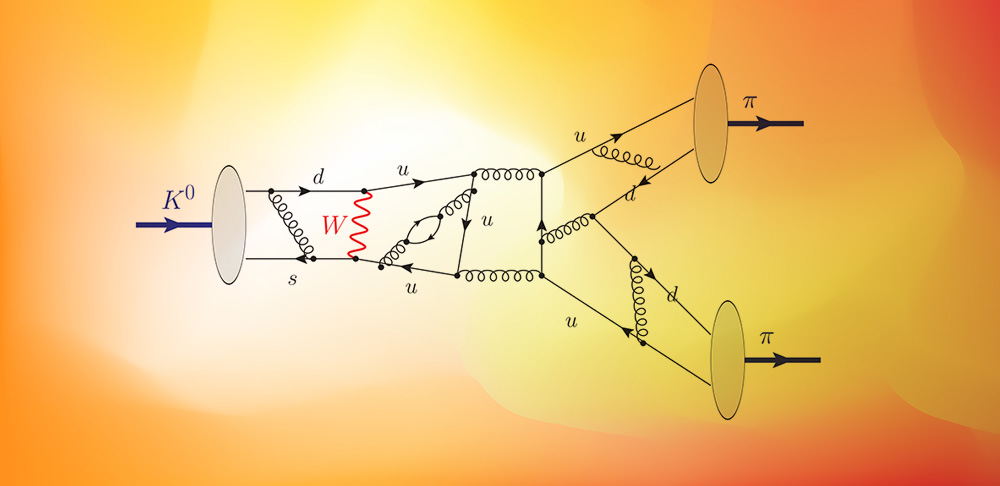
When the neutral kaon (containing a strange quark) decays, it typically results in the net production of either two or three pions. Supercomputer simulations are required to understand whether the level of CP-violation, first observed in these decays, agrees or disagrees with the Standard Model’s predictions. With the exception of only a few particles and particle combinations, almost every set of particles in the Universe are unstable, and if they don’t annihilate away, they will decay in short order.

There are also rules that must be followed in order for any sort of composite particle to exist: the full suite of the quantum rules that govern the Universe.

• Energy must be conserved, meaning that if you wish to create a particle initially, you must have enough available energy (via Einstein’s E = mc²) for that particle to be able to be created.
• Electric charge, angular momentum, linear momentum, and other quantum properties must also be conserved: you can only create particles (or particle-antiparticle pairs) that don’t violate these conservation laws.
• Rules about spin, or the inherent angular momentum of these particles, must be obeyed, including as respects the decay pathways of parent particles into daughter particles.
• And if you have any quark-and-gluon containing entity, which are the only particles that experience the strong nuclear force, you can only create a “colorless” combination of these particles, even for an instant, if you want them to exist.

The rules about the strong nuclear force and color are a little bit more complicated than theories with only one type of charge (positive and attractive, like gravity) or two types of charge (positive and negative, where like charges repel and opposite charges attract, like electromagnetism), and involve three fundamental types of charge — color charge — that are all interrelated. While every quark has a color, every antiquark has an anticolor, and every gluon carries a color-anticolor combination, the bound states that exist must all be truly colorless.

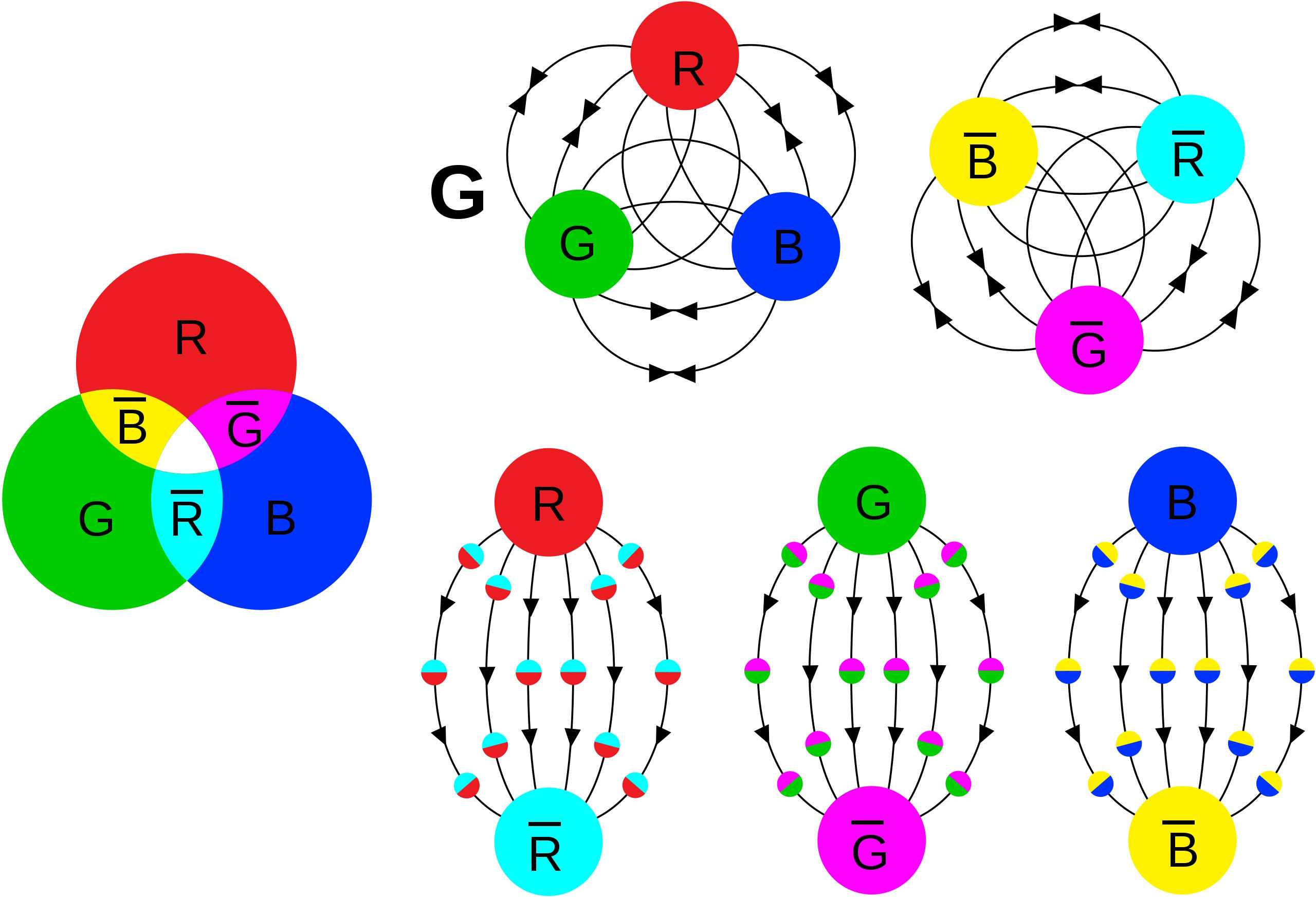
Combinations of three quarks (RGB) or three antiquarks (CMY) are colorless, as are appropriate combinations of quark/antiquark pairs. The gluon exchanges that keep these entities stable are quite complicated, but require eight, not nine, gluons. Particles with a net color charge are forbidden under the strong interactions.

This leaves us, perhaps surprisingly to some, with an enormous number of possible combinations for creating colorless bound states.

• You can have a color-anticolor combination, like a quark-antiquark pair, to make a meson.
• You can have a color-color-color or anticolor-anticolor-anticolor combination, such as three quarks or three antiquarks, to make either a baryon or an anti-baryon.
• You can have multiple combinations of either or both of the two above options to still maintain a colorless state; so long as there are equal numbers of “colored” and “anticolored” particles, or that there’s an excess of one type over the other in multiples of three, you can have a colorless entity, including tetraquarks, pentaquarks, hexaquarks, or greater numbers or quarks.
• Or you can have something that’s made exclusively of gluons — the particles that carry a color-anticolor combination inherently — with no quarks or antiquarks at all, save for the ones that arise internally as a consequence of the gluon field.

That last possibility is rarely discussed in particle physics, because the resultant entity — a glueball — had not only never been detected, but calculating the expected properties of glueballs was too daunting of a task for 20th century physicists.

Today, Feynman diagrams are used in calculating every fundamental interaction spanning the weak and electromagnetic forces, including in high-energy and low-temperature/condensed conditions. Including higher-order “loop” diagrams leads to more refined, more accurate approximations of the true value to quantities in our Universe. However, the strong interactions cannot be computed in this fashion, and must either be subject to non-perturbative computer calculations (Lattice QCD) or require experimental inputs (the R-ratio method) in order to account for their contributions.

But here in the 21st century, we can do those calculations. The difference is that, in the 20th century, the only reliable technique we had for calculating the properties of quantum systems was perturbatively: where you calculate progressively more and more complex interaction terms to get progressively more and more accurate answers. This approach, which was so successful for quantum electrodynamics (where the interaction strength gets smaller at greater distances and has a small coupling constant at low energies), fails spectacularly for quantum chromodynamics, as the strong force gets greater as distances increase and its coupling constant is large.

However, a new technique came along with the advent of high-performance computing: the technique of Lattice QCD. By treating spacetime as a discrete grid with a very small inherent spacing, we can make predictions for larger-scale phenomena: the confinement of QCD bound states, the conditions under which a quark-gluon plasma should arise, and even a prediction for the masses of various bound states, including not only the proton and neutron, but heavy and exotic bound states as well. In other words, whereas we couldn’t calculate the full suite of the expected properties of tetraquarks, pentaquarks, and glueballs back in the 1990s, those are calculation we can perform — down to precisions with only a few percent uncertainty — here in the 2020s.

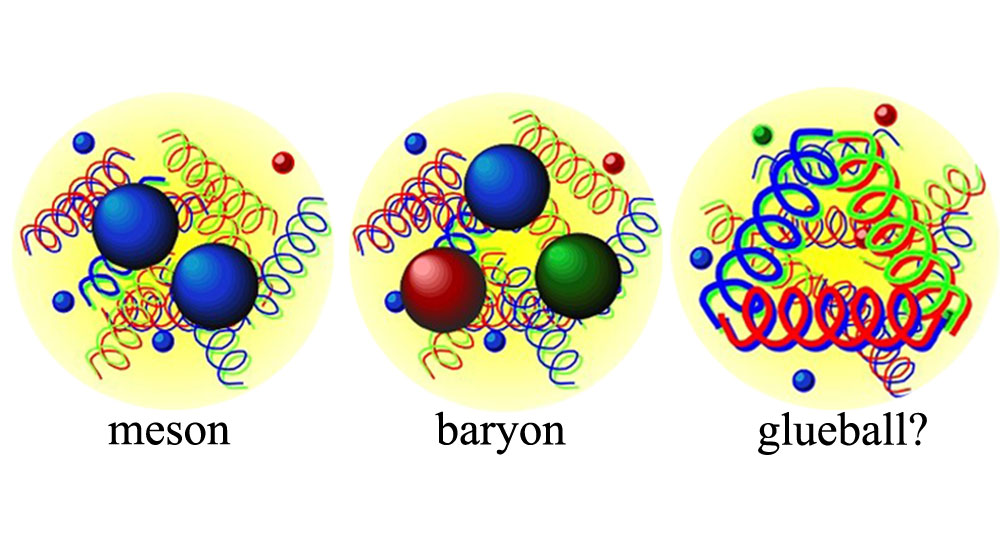
Gluons aren’t simply the particles that bind quarks together; they may also be particles that bind themselves together into a quarkless glob known as a glueball. The lightest glueball state may be able to be revealed from the decays of particles created in electron-positron colliders.

Theoretically, these predictions now include one for the lightest glueball state: it should be a pseudoscalar, with total spin 0, no electric charge, and with odd parity, and with a rest mass of between 2.3 and 2.6 GeV/c². If you want to try and create this glueball state experimentally, your best bet is to create a composite particle whose mass is slightly greater than this value, but whose decay produces lots of gluons and hadrons: an ideal place for searching for glueballs. Because of how easy it is to produce it with modern technology, and because it has precisely these properties, decays of the J/ψ particle is generally regarded as a great place to look for these potential glueball states.

Whenever a J/ψ particle is created, there’s about a 26% chance that it will decay into a photon (which can then decay into either quark-containing particles or lepton-antilepton pairs), about a 64% chance it will decay into three gluons, and about a 9% chance it will decay into a photon and two gluons. Even though most of the decays are mundane and well-understood, a small contribution from the lightest glueball could contribute to some of these decay channels. In particular, if a J/ψ particle decays into:

• a photon,
• an η′ particle,
• and either a pair of kaons or a pair of pions,

a resonance of the η′ with the kaon/pion pair could appear in the data if it corresponds to the lightest glueball state.

The BES III Experiment at the Beijing Electron-Positron Collider 2 in China collides electrons and positrons at energies between 2 and 4.7 GeV to create a variety of known and previously unknown particles, including exotic QCD states. The discovery of multiple tetraquark states has already come from this collaboration, and the X(2370) now emerges as an exciting candidate for a possible glueball particle.

The greatest “factory” ever constructed for investigating the J/ψ particle is located in Beijing at their electron-positron collider, known as the Beijing Spectrometer III (BES III), which began taking data in its modern form in 2008. In its first year, alone, BES III accumulated some 226 million events that created J/ψ particles, and as of the end of 2023, that cumulative number now exceeds 10 billion J/ψ particles. Therefore, even rare events and resonances that emerge from these decays can now be probed. A few exotic states have been discovered as well: a class of particles known as XYZ mesons, which are now known to include exotic states such as tetraquarks.

All told, with the data collected at BES III, they can announce definitive evidence for a new composite particle known as the X(2370), with:

• a mass of 2.395 GeV/c²,
• a spin of 0,
• a branching fraction of approximately 0.000013 [meaning that about 1 out of every 76,000 J/ψ particles will decay into something that includes an X(2370)],
• and that appears with a cumulative statistical significance of a whopping 11.7-σ.

In particle physics, a result that appears with more than 5-σ significance has just a 0.00006% chance of being a statistical fluke, and any result more significant than that has surpassed the “gold standard” for announcing a bona fide discovery.

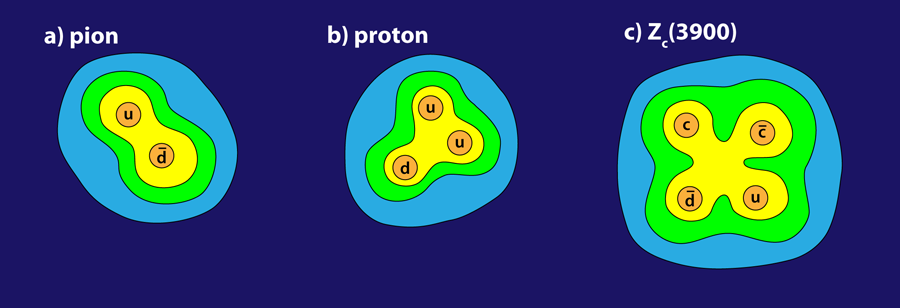
Originally, the only hadrons known to exist were either combinations of three quarks (baryons), three antiquarks (anti-baryons), and quark-antiquark pairs (mesons). Now, more exotic states such as tetraquarks, including the Z_c(3900) shown here, are known to exist as well. Glueballs, pentaquarks, and other exotics remain tantalizing and expected possibilities as well.

Although the particle was first announced as being at 2.370 GeV/c², which is why it’s known as the X(2370), the latest experimental results indicate that its mass is more accurately 2.395 GeV/c², with an experimental uncertainty of 0.011 GeV/c² attached to it. Meanwhile, the latest theoretical results from Lattice QCD, published in 2019, predicted a mass of 2.395 ± 0.014 GeV/c², which shows a spectacular agreement between experiment and theory. This particle, the X(2370), exists, and is having its properties measured better than ever before, with this latest study being the first to measure the quantum numbers of its spin and parity.

While all of it is consistent with this particle being the first glueball ever detected, however, there are still reasons to be cautious. For one, other X-mesons have been discovered, and are mere resonances involving combinations of quarks-and-antiquarks rather than glueballs. For another, the production rate of the X(2370) observed from J/ψ decays is a bit too high to be consistent with the glueball interpretation, although that interpretation is still being reviewed. And finally, the negative parity measured for X(2370) is consistent with this being a pseudoscalar instead of a scalar, but this only establishes a consistency with the glueball interpretation: not a smoking gun signal that it is indeed a glueball in its nature.

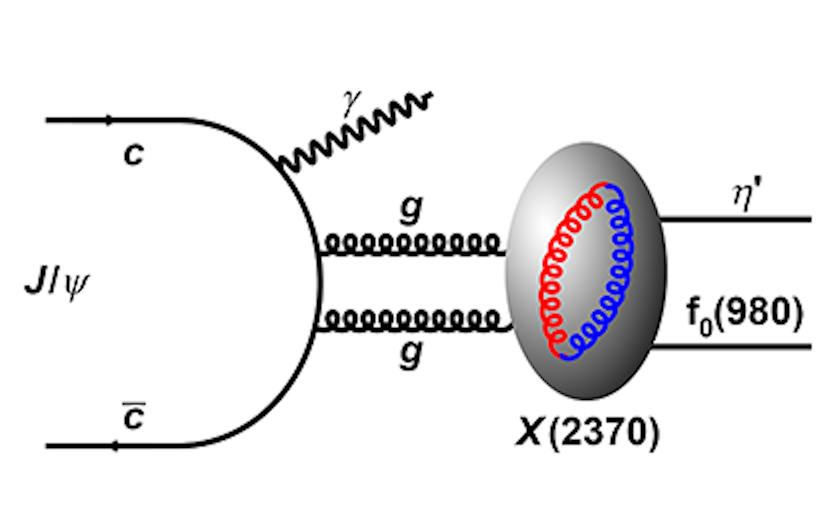
The J/ψ system can decay to a photon and two gluons, where the two gluons can then combine to temporarily create an X(2370) exotic particle. Although its nature is still not 100% certain, the interpretation of the X(2370) as a glueball remains compelling, and if so, it would be the first glueball particle ever revealed by experiment.

The big question at the core of this study is whether glueballs exist or not, as the Standard Model and the theory of QCD predict that they must, and whether the observations of the X(2370) are sufficient to establish it as a glueball state itself. These latest results — the strongest and most robust in history — support the interpretation of the X(2370) as a potential glueball state, and bring us one step closer to putting this key aspect of the Standard Model to a critical test. However, until questions about its production rate and branching ratios can be sufficiently answered, we have to remain open-minded to the fact that this could be just another “exotic” state, like a tetraquark, that isn’t composed solely of gluons.

Nevertheless, with the production of many hundreds of thousands of X(2370) particles as the result of the decay of more than 10 billion J/ψ particles, we have now solidly measured more properties than ever of this exotic particle. It is now the most compelling, interesting candidate for a glueball: a species of composite particle that should exist, but that has never been seen before. More work still needs to be done to determine the full nature of the X(2370) particle, but this is the strongest evidence for the existence of a glueball ever put forth into the world. If no glueballs exist in all of nature, then something new is wrong with the Standard Model. If glueballs do exist, however, the X(2370) just might be the first one revealed to humanity.